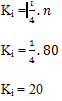PENDAHULUAN
A.
Latar belakang masalah
Statistik merupakan sebuah metoda perhitungan yang
mampu membantu banyak kalangan manusia pada saat ini. Baik dalam kehidupan
secara umum, sekolah, perkuliahan, perkantoran dan lain sebagainya. Tidak hanya
sampai di sana, statistik juga digunakan untuk membantu dalam hal penelitian,
bahkan membuat karya ilmiah seperti skripsi, tesis dan disertasi. Hal ini juga
diungkapkan Riduwan (2009), “statistik merupakan alat untuk mempermudah
perhitungan angka-angka atau data. Dari berbagai kehidupan akan membutuhkan
statistik untuk menganalisis sesuatu”.
|
Berdasarkan
penjelasan di atas, jelas statitik memiliki banyak manfaat bagi manusia,
termasuk juga dalam pembuatan karangan ilmiah. Dalam pembuatan karangan ilmiah
begitu banyak materi-materi dari statistik yang digunakan, mulai dari
distribusi frekuensi, uji t, korelasi, regresi, ukuran letak (ukuran lokasi)
dan lain sebagainya, yang digunakan
untuk membantu memudahkan dalam pengolahan data dari hasil penelitian
terutama pada penelitian kuantitatif. Dalam penelitian tersebut, statistik
sangatlah peran penting. Untuk itu sudah semestinya semua kalangan mempelajari
statistik agar mampu menerapkannya untuk kebutuhan tertentu. Terutama untuk
siswa dan juga mahasiswa serta ilmuan. Pada dasarnya diharapkan mahasiswa lebih
memahi statistik serta berbagai macam materi-materi yang terkandung di dalam
statistik tersebut tersebut, salah satunnya ukuran lokasi (ukuran letak).
Menurut Andi (2007: 69), ukuran lokasi (ukuran letak) dimaksudkan sebagai
besaran atau ukuran untuk mendapatkan gambaran yang lebih jelas berdasarkan
letak data dari sekumpulan data yang dipunyai. Ukuran ini sangat berarti dalam
rangka melakukan analisis data.
Berdasarkan ungkapan di atas, jelas salah satu materi
yang dibahas di dalam statistik yaitu ukuran lokasi sangatlah diperlukan untuk
membantu menganalisis suatu data. Berdasarkan hal itu juga mahasiswa dituntut
untuk mengetahui bagaimana pembahasan mengenai ukuran lokasi tersebut baik
kuartil, desil maupun persentil agar mampu menganalisis data pada saat
penelitian dan penyusunan karya akhir.
Namun berdasarkan realita saat ini, mahasiswa masih
belum mampu untuk memahami materi-materi yang terkandung di dalam statistik
seperti korelasi, distribusi frekuensi, regresi, dan terutama juga ukuran letak
(ukuran lokasi). Pada pembelajaran ini juga banyak mahasiswa yang merasa tidak
begitu memahami apa yang ada dalam materi tersebut. Serta yang paling ,menyita
perhatian ialah banyak kalangan mahasiswa yang rela membayar pembuatan karya ilmiah atau menganalisis data kepada
orang lain hanya untuk menyelesaikan suatu kewajiban akhir dari kuliah. Melihat
dari kejadian itu, penulis tertarik
untuk membahas sekaligus membantu mahasiswa lainnya untuk dapat memahami
tentang statisstik terutama pada materi atau pembahasan ukuran lokasi (ukuran
letak). Maka dari itu penulis akan membuat sebuah makalah yang berjudul “
Ukuran Lokasi (Ukuran Letak)”. Diharapkan mampu membantu mahasiswa lain untuk
memahami materi ini.
B.
Identifikasi masalah
Berdasarkan latar belakang masalah di atas,
maka masalah dapat diidentifiakasikan sebagai berikut:
1. Kurangnya pemahaman mahasiswa terhadap
statistik
2. Kurangnya pemahaman mahasiswa terhadap materi
statistik terutama ukuran lokasi.
C.
Pembatasan masalah
Berdasarkan identifikasi masalah di atas, serta
mengingat begitu luas masalah tentang statistik ini. Maka penulis berkesimpulan
untuk membatasi pembahasan makalah ini menjadi Ukuran Lokasi (ukuran letak).
D.
Tujuan pembahasan
Berdasarkan hal di atas, maka dapat dikatakan tujuan
pembahasan ini adalah:
1. Agar mahasiswa lebih memahami mata kuliah statistik.
2. Agar mahasiswa lebih memahami materi yang membahas
tentang ukuan lokasi.
3. Diharapkan pembahasan ini mampu membantu dalam
penyelesaian tugas akhir.
E.
Manfaat pembahasan
Adapun beberapa manfaat dari pembahasan makalah ini
adalah sebagai berikut:
1. Memenuhi tuntutan tugas makalah Statistik I yang
berjudul ”Ukuran Lokasi (ukuran letak).
2. Sebagai pembelajaran bagi penulis dan juga pembaca
serta mahasiwa lainnya.
3. Sebagai pendukung bahan ajar terutama dalam mata
kuliah statistik ini.
PEMBAHASAN
A.
Pengertian Ukuran Lokasi (Location Measurement)
Menurut Andi (2007: 69), Ukuran lokasi (ukuran letak)
dimaksudkan sebagai besaran atau ukuran untuk mendapatkan gambaran yang lebih
jelas berdasarkan letak data dari sekumpulan data yang dipunyai. Ukuran ini
sangat berarti dalam rangka melakukan analisis data.
Berdasarkan penjelasan di atas, maka dapat diartikan
bahwa ukuran lokasi (ukuran letak) merupakan ukuran untuk melihat dimana letak
salah satu data dari sekumpulan banyak data yang ada. Andi juga di dalam
bukunya (2007: 69) menjelaskan bahwa, yang termasuk ukuran lokasi (ukuran
letak) antara lain adalah kuartil, desil dan persentil.
B.
Bagian-bagian Ukuran Lokasi
1.
Kuartil (Kuartiles)
Secara umum kuartil
merupakan sekumpulan data yang dibagi menjadi empat bagian yang sama banyak,
sesudah disusun menurut urutan nilainya, maka bilangan pembaginya disebut
kuartil. Pengertian kuartil di atas juga didukung oleh Andi (2007: 80) menyebutkan, nilai kuartil merupakan nilai
dari sekumpulan data yang dibagi menjadi empat bagian yang sama, dan yang
membagi data tersebut dinamakan kuartil. Selain itu juga terdapat pengertian
lainnya yang menyebutkan kuartil merupakan nilai atau angka yang membagi data
terkecil sampai data terbesar atau sebaliknya dari data terbesar sampai data
terkecil, (Riduwan, 2009: 104).
Menurut Andi (2007:
80), menyebutkan Ada tiga buah kuartil, yakni kuatil pertama, kuartil kedua,
dan kuartil ketiga yang masing-masing disingkat dengan K1, K2,
dan K3. Pemberian nama ini dimulai dari nilai kuartil paling kecil.
Untuk menentukan nilai kuartil dapat dilakukan dengan dua kategori yaitu, nilai
kuartil yang belum dikelompokkan (data tunggal), dan juga data yang sudah
dikelompokkan (data kelompok).
a. Kuartil Data Tunggal
Menurut Andi (2007: 80), pada bukunya menyebutkan untuk
menentukan nilai kuartil yang belum dikelompokkan (data tunggal) memiliki
beberapa langkah-langkah, yaitu sebagai berikut:
1) langkah pertama
menyusun data, dengan mengurutkan data dimulai dari yang terkecil sampai yang
terbesar.
2) Menentukan letak kuartil yang diminta dengan
menggunakan rumus:
Keterangan:
Ki =
kuartil ke –
n = jumlah data
i = letak kuartil
Berikut ini adalah
contoh dari Kuartil data tunggal dengan data perumpaan nilai statistik I
sebanyak 10 mahasiswa: 60, 80, 90, 70, 85, 95, 75, 65, 50, 55. Tentukanlah
nilai kuartil K1 dan K3.
Penyelesaian :
Langkah penyelesaian
1) Mengurutkan data dari
yang terendah (terkecil) sampai terbesar (tertinggi).
50, 55, 60, 65, 70,
75, 80, 85, 90, 95
2) Tentukan letak
kuartil K1 dan K3 dengan penjelasan seperti di bawah ini:
a) Menentukan K1,
Dari hasil di atas, maka
data ke 2,75 berada diantara data 2 dan 3 sehingga menjadi seperti berikut :
K1 = data
ke- 2 + 0,75 (data ke- 3 – data ke- 2)
K1 = 55 +
0,75 (60 – 55)
K1 = 55 + 3,75
K1 = 58,5
Berdasarkan hasil
perhitungan di atas, maka posisi K1 menunjukkan nilai 58,5.
Dari hasil di atas, maka data ke 8,25 berada diantara data 8 dan 9 sehingga menjadi seperti berikut :
K3 = data
ke- 8 + 0,25 (data ke- 9 – data ke- 8)
K3 = 85 +
0,25 (90 – 85)
K3 = 85 +
1,25
K3 = 86, 25
Berdasarkan hasil perhitungan di atas, maka posisi K3 menunjukkan
nilai 86,25.
b. Kuartil data berkelompok
Mencari kuartil dalam
bentuk data berkelompok terlebih dahulu adanya tabel distribusi frekuensi. Hal
ini juga disampaikan oleh Riduwan (2009: 106), menyebutkan bahwa mencari
kuartil data kelompok haruslah dibuat susunan distribusi frekuensi terlebih
dahulu, dalam hal ini semata-mata untuk mempermudah perhitungan. Selain itu
Riduwan juga menerangkan langkah-langkah
pembuatan tabel distribusi frekuensi (2009: 106), yaitu:
1) Menyusun data dari
yang terkecil sampai yang terbesar
2) Menghitung rentang (range)
3) Jumlah kelas
4) Dan panjang kelas
intervalnya.
Setelah tabel
distribusi terbentuk, maka dilanjutkan dengan mencari nilai kuartil dengan
rumus yang diungkapkan Andi (2007: 81), seperti berikut:
Keterangan:
b = Tepi
bawah interval kelas Ki ( b = batas bawah - 0,5)
p =
Panjang kelas interval
i = Letak Ki
n =
Banyak data
F =
Frekuensi kumulatif sebelum kelas Ki
f =
Frekuensi pada kelas Ki
Berikut ini adalah
contoh dari kuartil data kelompok, buatlah tabel
distribusi frekuensi dan hitunglah kuartil K1 dan K2 dari data di bawah
ini:
29
|
43
|
43
|
48
|
49
|
51
|
56
|
60
|
60
|
60
|
61
|
63
|
63
|
63
|
65
|
66
|
67
|
67
|
68
|
70
|
70
|
70
|
70
|
71
|
71
|
71
|
72
|
72
|
72
|
73
|
73
|
74
|
74
|
74
|
74
|
75
|
75
|
76
|
76
|
77
|
78
|
79
|
79
|
80
|
80
|
80
|
80
|
81
|
81
|
81
|
82
|
82
|
83
|
83
|
83
|
84
|
85
|
86
|
86
|
87
|
88
|
88
|
88
|
88
|
89
|
90
|
90
|
90
|
91
|
91
|
91
|
92
|
92
|
93
|
93
|
93
|
95
|
97
|
98
|
98
|
Penyelesaian:
Adapun
langkah-langkah dalam penyelesaian ialah sebagai berikut:
1) Langkah pembuatan
tabel distribusi frekuensi
a) Menentukan range
(rentang)
R = nilai max – nilai
min
R = 98 -29 = 69
b) Menentukan jumlah
kelas
K = 1+Log n. 3,3
K = 1+Log 80. 3,3
K = 7,3
c) Menentukan panjang
kelas interval
Tabel 1. Distribusi frekuensi nilai statistik I
Nilai Statistik
|
F
|
F kumulatif
|
29-38
|
1
|
1
|
39-48
|
3
|
4
|
49-58
|
3
|
7
|
59-68
|
12
|
19
|
69-78
|
22
|
41
|
79-88
|
23
|
64
|
89-98
|
16
|
80
|
Jumlah
|
80
|
-
|
2) Langkah-langkah
menentukan nilai K1 dan K 2
a) Berdasarkan tabel di
atas, maka letak K1 Letak dapat dihitung seperti di bawah ini :
(1) Menentukan letak
kelas interval
(2) Menentukan batas
bawah
Berdasarkan hal di
atas, maka langkah selanjutnya adalah memasukkan angka-angka terebut ke dalam rumus untuk mencari nilai K1
Jadi berdasarkan dari perhitungan di atas, maka nilai
kuartil K1 yang didapat adalah: 68,95.
b) Berdasarkan tabel di atas,
maka letak K2 Letak dapat
dihitung seperti di bawah ini :
(1) Menentukan letak
kelas interval
Dari hasil
perhitungan di atas, maka data ke- 40 berada pada kelas 69-78 atau terletak pada kelas interval ke- 5.
(1) Menentukan batas
bawah
Berdasarkan hal di
atas, maka langkah selanjutnya adalah memasukkan angka-angka tersebut ke dalam rumus untuk mencari nilai K2
Jadi berdasarkan dari perhitungan di atas, maka nilai
kuartil K2 yang didapat adalah: 78.
2.
Desil (Deciles)
“ Ds”
Jika sekumpulan data dibagi menjadi 10 bagian yang
sama, maka didapat sembilan pembagi dan tiap pembagi dinamakan desil. Karenanya
ada sembilan buah desil, ialah D1, D2, …, D9. Hal
ini diperkuat oleh Riduwan (2009: 111),
menyatakan desil (Ds) ialah nilai atau angka yang membagi data yang menjadi 10
bagian yang sama, setelah disusun dari data terkecil sampai data terbesar atau
sebaliknya.
Berdasarkan
penjelasan di atas, maka data diartikan bahwa desil (Ds) merupakan angka
yang membagi data menjadi 10 bagian yang
sama setelah melalui penyusunan data
terlebih dahulu. Data itu dapat disusun dimulai dari angka terkecil sampai
dengan angka terbesar. Menurut Riduwan pada bukunya (2009: 111), menyebutkan
bahwa cara mencari desil hampir sama dengan mencari kuartil hanya bedanya
terletak pada pembagian saja.
Harga-harga desil di wakili dengan:
D1, D2, D3, . . . . . . . . . . D9. Untuk
menentukan nilai desil dapat dilakukan dengan dua kategori yaitu, nilai desil
yang belum dikelompokkan (data tunggal), dan juga data yang sudah dikelompokkan
(data kelompok).
a.
Desil data tunggal
Menurut Andi (2007: 82), pada bukunya menyebutkan
untuk menentukan nilai desil yang belum
dikelompokkan (data tunggal)
1) langkah pertama
menyusun data, dengan mengurutkan data dimulai dari yang terkecil sampai yang
terbesar.
2) Menentukan letak desil yang diminta dengan menggunakan
rumus:
Keterangan:
Di =
desil ke –
n = jumlah data
i = urutan desil
Berikut ini adalah
contoh dari desil data tunggal : dengan data perumpaan nilai statistik I
sebanyak 10 mahasiswa: 60, 80, 90, 70, 85, 95, 75, 65, 70, 65. Tentukanlah
nilai desil Ds3 dan Ds6.
Penyelesaian :
Langkah penyelesaian
1) Mengurutkan data dari
yang terendah (terkecil) sampai terbesar (tertinggi).
60, 65, 65, 70, 70,
75, 80, 85, 90, 95
2) Tentukan letak desil Ds3
dan Ds6 dengan penjelasan seperti di bawah ini:
a) Menentukan Ds3,
Dari hasil di atas, maka data ke 3,3 berada di antara data 3 dan 4 sehingga menjadi seperti berikut :
Ds3 = data
ke- 3 + 0,30 (data ke- 4 – data ke- 3)
Ds3 = 65 +
0,30 (70 – 65)
Ds3 = 65 +
1,5
Ds3 = 66,5
Berdasarkan hasil
perhitungan di atas, maka posisi Ds3 menunjukkan
nilai 66,5.
b) Menentukan D6,
Dari hasil di atas, maka data ke- 6,6 berada di antara data 6 dan 7 sehingga menjadi seperti berikut :
D6 = data
ke- 6 + 0,6 (data ke- 7 – data ke- 6)
D6 = 75 +
0,6 (80 – 75)
D6 = 75 +
3
D6 = 78
Berdasarkan hasil
perhitungan di atas, maka posisi D3
menunjukkan nilai 78.
b.
Desil data berkelompok
Mencari desil dalam bentuk data berkelompok terlebih dahulu
dengan adanya tabel distribusi frekuensi. Hal ini juga disampaikan oleh Riduwan
(2009: 112), menyebutkan bahwa mencari desil data berkelompok haruslah dibuat
susunan dristribusi frekuensi terlebih dahulu, dalam hal ini semata-mata untuk
mempermudah perhitungan. Selain itu Riduwan juga menerangkan langkah-langkah
pembuatan tabel distribusi frekuensi (2009: 112), yaitu:
1) Menyusun data dari
yang terkecil sampai yang terbesar
2) Menghitung rentang (range)
3) Jumlah kelas
4) Dan panjang kelas
intervalnya.
Setelah tabel distribusi frekuensi terbentuk, maka dilanjutkan dengan mencari nilai desil dengan rumus yang diungkapkan Andi (2007: 83), seperti berikut:
Keteragan:
b = Tepi
bawah interval kelas Dsi ( b = batas bawah - 0,5)
p =
Panjang kelas interval
i = letak Dsi
n =
Banyak data
F = Frekuensi kumulatif sebelum kelas Dsi
f = Frekuensi pada kelas Dsi
Berikut ini adalah
contoh dari desil data berkelompok, buatlah tabel
distribusi frekuensi dan hitunglah desil
Ds4 dan Ds7 dari data nilai statistik I di bawah
ini:
29
|
43
|
43
|
48
|
49
|
51
|
56
|
60
|
60
|
60
|
61
|
63
|
63
|
63
|
65
|
66
|
67
|
67
|
68
|
70
|
70
|
70
|
70
|
71
|
71
|
71
|
72
|
72
|
72
|
73
|
73
|
74
|
74
|
74
|
74
|
75
|
75
|
76
|
76
|
77
|
78
|
79
|
79
|
80
|
80
|
80
|
80
|
81
|
81
|
81
|
82
|
82
|
83
|
83
|
83
|
84
|
85
|
86
|
86
|
87
|
88
|
88
|
88
|
88
|
89
|
90
|
90
|
90
|
91
|
91
|
91
|
92
|
92
|
93
|
93
|
93
|
95
|
97
|
98
|
98
|
Penyelesaian:
Adapun
langkah-langkah dalam penyelesaian ialah
sebagai berikut:
1) Langkah pembuatan
tabel distribusi
a) Menentukan range
(rentang)
R = nilai max – nilai
min
R = 98 - 29 = 69
b) Menentukan jumlah kelas
K = 1+Log n. 3,3
K = 1+Log 80. 3,3
K = 7,3
c) Menentukan panjang
kelas interval
Tabel 2. Distribusi frekuensi nilai statistik I
Nilai Statistik
|
F
|
F kumulatif
|
29-38
|
1
|
1
|
39-48
|
3
|
4
|
49-58
|
3
|
7
|
59-68
|
12
|
19
|
69-78
|
22
|
41
|
79-88
|
23
|
64
|
89-98
|
16
|
80
|
Jumlah
|
80
|
-
|
2) Langkah-langkah menentukan nilai Ds4 dan Ds7
a) Berdasarkan tabel di
atas, maka letak D4 dapat dihitung seperti di bawah ini :
(1) Menentukan letak
kelas interval dari nilai D4
Dari hasil
perhitungan di atas, maka data ke- 32 berada pada kelas 69-78 atau
terletak pada kelas interval ke- 5.
(2) Menentukan batas
bawah
Berdasarkan hal di
atas, maka langkah selanjutnya adalah memasukkan angka-angka tersebut ke dalam rumus untuk mencari nilai Ds4
Jadi berdasarkan dari perhitungan di atas, maka nilai
desil Ds4 yang didapat adalah: 74,4.
b) Berdasarkan tabel di
atas, maka letak Ds7 dapat dihitung seperti di bawah ini :
(1) Menentukan letak
kelas interval
Dari hasil perhitungan di atas, maka data ke- 56 berada pada kelas 79-88 atau terletak pada kelas interval ke- 6.
(2) Menentukan batas
bawah
Berdasarkan hal di
atas, maka langkah selanjutnya adalah
memasukkan angka-angka tersebut
ke dalam rumus untuk mencari nilai Ds7
Jadi berdasarkan dari perhitungan di atas, maka nilai
desil Ds7 yang didapat
adalah: 85
3.
Persentil (Percentiles)
“Ps”
Sekumpulan data yang dibagi menjadi 100 bagian yang
sama, akan menghasilkan 99 pembagi berturut-turut yang dinamakan persentil
pertama, persentil kedua, …, persentil ke- 99. Penjelasan di atas
juga didukung oleh Riduwan (2009: 114), menyatakan persentil (Ps) ialah nilai
yang membagi data menjadi 100 bagian yang sama. Setelah disusun dari angka
terkecil sampai ke yang terbesar. Harga persentil ada 99 bagian yaitu Ps1,
Ps2, Ps3, ......., Ps99. Penjelasan lain juga disampaikan oleh Andi (2007: 85),
menyatakan nilai persentil merupakan nilai yang sekumpulan data yang dibagi
menjadi seratus bagian yang sama, dan yang membagi data tersebut dinamakan
persentil.
Berdasarkan penjelasan di atas, maka dapat dikatakan
bahwa persentil merupakan nilai dari sekumpulan data yang dibagi menjadi 100
bagian yang sama. Selain itu persentil memiliki 99 bagian, dimulai dari Ps1
sampai dengan Ps99. Menurut
Andi (2007: 85), untuk menentukan nilai-nilai persentil tersebut dapat dibagi
menjadi dua yaitu data yang belum dikelompokkan (data tunggal) dan data yang sudah
dikelompokkan (data kelompok).
a. Persentil data
tunggal
Menurut Andi (2007: 82), pada bukunya menyebutkan
untuk menentukan nilai persentil yang
belum dikelompokkan (data tunggal), memiliki beberapa langkah-langkah, yaitu:
1) Langkah pertama
menyusun data, dengan mengurutkan data dimulai dari yang terkecil sampai yang
terbesar.
2) Menentukan letak persentil yang diminta dengan
menggunakan rumus:
Keterangan:
Pi =
persentil ke –
n = jumlah data
i = urutan persentil
perhatikanlah contoh Berikut
ini tentang data tunggal : dengan data perumpaan nilai statistik I sebanyak 12
mahasiswa: 50, 55, 60, 80, 90, 70, 85, 95, 75, 70, 70, 65. Tentukanlah nilai
persentil Ps22 dan Ps73
Penyelesaian :
Langkah penyelesaian
1) Mengurutkan data dari
yang terendah (terkecil) sampai terbesar (tertinggi).
50, 55, 60, 65, 70,
70, 70, 75, 80, 85, 90, 95
2) Tentukan letak
persentil Ps22 dan Ps93 dengan penjelasan seperti di
bawah ini:
a) Menentukan Ps22,
Dari hasil perhitungan di atas, maka data ke- 2,86 berada di antara data 2 dan 3 sehingga menjadi seperti berikut :
Ps22 =
data ke- 2 + 0,86 (data ke- 3 – data ke- 2)
Ps22 = 55
+ 0,86 (60 – 55)
Ps22 = 55
+ 4,3
Ps22 = 59,3
Berdasarkan hasil perhitungan di atas, maka posisi Ps22
menunjukkan nilai 59,3.
b) Menentukan D93,
Dari hasil di atas,
maka data ke- 9,49 berada di antara data 9 dan 10 sehingga menjadi seperti
berikut :
Ps73 =
data ke- 9 + 0,49 (data ke- 10 – data ke- 9)
Ps73 = 80
+ 0,49 (85 – 80)
Ps73 = 80
+ 2,45
Ps73 = 82,45
Berdasarkan hasil
perhitungan di atas, maka posisi Ps73
menunjukkan nilai 82,45.
b. Persentil data
berkelompok
Mencari persentil
dalam bentuk data berkelompok terlebih dahulu dengan adanya tabel distribusi
frekuensi. Hal ini juga disampaikan oleh Riduwan (2009: 116), menyebutkan bahwa
mencari persentil data berkelompok haruslah dibuat susunan dristribusi frekuensi
terlebih dahulu, dalam hal ini semata-mata untuk mempermudah perhitungan.
Selain itu Riduwan juga menerangkan langkah-langkah pembuatan tabel distribusi
frekuensi (2009: 116), yaitu:
1) Menyusun data dari
yang terkecil sampai yang terbesar
2) Menghitung rentang (range)
3) Jumlah kelas
4) Dan panjang kelas
intervalnya.
Setelah tabel distribusi terbentuk, maka dilanjutkan dengan mencari nilai persetil dengan rumus yang diungkapkan Andi (2007: 86), seperti berikut:
b =
Tepi bawah interval kelas Psi ( b = batas bawah - 0,5)
p =
Panjang kelas interval
i =
letak Psi
n =
Banyak data
F =
Frekuensi kumulatif sebelum kelas Psi
f =
Frekuensi pada kelas Psi
Berikut ini adalah
contoh dari persentil data berkelompok, buatlah tabel
distribusi dan hitunglah persentil Ps20
dari data nilai statistik I dibawah ini:
29
|
43
|
43
|
48
|
49
|
51
|
56
|
60
|
60
|
60
|
61
|
63
|
63
|
63
|
65
|
66
|
67
|
67
|
68
|
70
|
70
|
70
|
70
|
71
|
71
|
71
|
72
|
72
|
72
|
73
|
73
|
74
|
74
|
74
|
74
|
75
|
75
|
76
|
76
|
77
|
78
|
79
|
79
|
80
|
80
|
80
|
80
|
81
|
81
|
81
|
82
|
82
|
83
|
83
|
83
|
84
|
85
|
86
|
86
|
87
|
88
|
88
|
88
|
88
|
89
|
90
|
90
|
90
|
91
|
91
|
91
|
92
|
92
|
93
|
93
|
93
|
95
|
97
|
98
|
98
|
Penyelesaian:
Adapun
langkah-langkah dalam penyelesaian ini, ialah sebagai berikut:
1) Langkah pembuatan
tabel distribusi
a) Menentukan range
(rentang)
R = nilai max – nilai
min
R = 98 -29 = 69
b) Menentukan jumlah
kelas
K = 1+Log n. 3,3
K = 1+Log 80. 3,3
K = 7,3
c) Menentukan panjang
kelas interval
Tabel 3. Distribusi frekuensi nilai statistik I
Nilai Statistik
|
F
|
F kumulatif
|
29-38
|
1
|
1
|
39-48
|
3
|
4
|
49-58
|
3
|
7
|
59-68
|
12
|
19
|
69-78
|
22
|
41
|
79-88
|
23
|
64
|
89-98
|
16
|
80
|
Jumlah
|
80
|
-
|
2) Langkah-langkah menentukan nilai Ps20
a) Berdasarkan tabel di
atas, maka letak Ps20 dapat dihitung seperti dibawah ini :
(1) Menentukan letak
kelas interval dari nilai Ps20
Dari hasil
perhitungan di atas, maka data ke- 16 berada pada kelas 59-68 atau
terletak pada kelas interval ke- 4.
(2) Menentukan batas
bawah
Berdasarkan hal di
atas, maka langkah selanjutnya adalah memasukkan angka-angka tersebut ke dalam rumus untuk mencari nilai Ps20
Jadi berdasarkan dari perhitungan di atas, maka nilai
dari persentil Ps20 yang didapat adalah: 66.
KESIMPULAN DAN SARAN
A.
Kesimpulan
Berdasarkan pembahasan pada bab sebelumnya maka
penulis dapat menyimpulkan bahwa Berdasarkan penjelasan di atas, maka dapat
diartikan bahwa ukuran lokasi (ukuran letak) merupakan ukuran untuk melihat
dimana letak salah satu data dari sekumpulan banyak data yang ada, yang
termasuk ukuran lokasi (ukuran letak) antara lain adalah kuartil, desil dan
persentil.
1. Kuartil, merupakan sekumpulan data yang dibagi menjadi
empat bagian yang sama banyak, sesudah disusun menurut urutan nilainya, maka
bilangan pembaginya.
2. Desil, ialah nilai atau angka yang membagi data yang
menjadi 10 bagian yang sama, setelah disusun dari data terkecil sampai data
terbesar atau sebaliknya.
3. Persentil ialah nilai
yang membagi data menjadi 100 bagian yang sama. Setelah disusun dari angka terkecil
sampai ke yang terbesar.
Pada ketiga bagian dari ukuran lokasi ini baik,
kuatil, desil, dan persentil dapat digolongkan dan dapat diselesaikan melalui
penggolongan pada data tunggal dan juga data kelompok.
|
B.
Saran
Berdasarkan pembahasan pada bab sebelumnya, penulis
ingin menyampaikan beberapa saran mengenai pembahasan ini, akan diuaraikan
sebagai berikut:
1. Dengan adanya pembahasan diharapkan bagi seluruh
pembaca, terutama pada diri penulis sendiri hendaknya lebih mempelajari
statistik terutama dalam pembahasan ukuran lokasi ataupun ukuran lokasi ini.
2. Diharapkan pada semu mahasiswa yang akan membuat
sebuah karya ilmiah diharapkan dengan aadanya pembahasan ini mampu mempelajari
lagi tentang statistik itu sendiri. Dengan adanya pemahaman tentang statistik
ini maka akan memudahkan dalam proses pengolahan data hasil penelitian yang
telah dilakukan.
DAFTAR
PUSTAKA
Andi. 2007. Statistika
“Data Kajian Deskriftif, Inferensi, dan Non Parametrik”. Jakarta:
Kencana Prenada Media Group.
Riduawan. 2009. Pengantar
statistika sosial. Bandung: Alfabeta.